Recursion and Fractals

There is endless fun to be had with recursion.


Sometimes it is hard to understand how a particular effect is produced.
The following procedure is an example of non-terminating tail recursion.

to inspi :a :d fd 20 rt :a inspi :a+:d :d end

Try it out with different inputs.
The procedure does not terminate itself you need to click the HALT button to stop it.

inspi 10 80
inspi 10 30
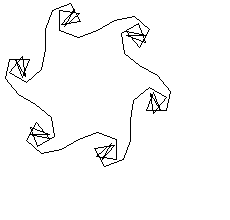
inspi 5 30

---

The procedure:

to staral :n if :n>300 [stop] fd :n rt 144 staral :n+5 end

is self-terminating and staral 5 produces:
The procedure:

to starshrink :n if :n<10 [stop] lt 18 star :n starshrink :n-15 end

which uses

to star :n repeat 5 [fd :n rt 144] end

is self-terminating and starshrink 200 produces

---

All the above are examples of "tail" recursion, that is the recursive call is placed at the end of a procedure.
A recursive call can in fact be placed anywhere in a procedure but if you do this you will have to also put in an "if" statement before the recursive call which will put a limit on the the variables involved or else the recursion will continue for ever. A recursive call within a procedure can be thought of as a "growth" call. The following examples illustrate how you can get images which have the property of being "self-similar."
This shape is produced by first writing the code for a simple Y shape and then inserting recursive calls at the two tips of the Y.

to treefrac :x if :x<2 [stop] fd :x lt 45 fd :x treefrac 2*:x/3 ;A "mini-tree" growing at the tip of the Y. bk :x rt 90 fd :x treefrac 2*:x/3 bk :x lt 45 bk :x End

The Y in the above shape is the "seed" and the recursive calls are "growth points" within the basic Y shape.
It is important that the basic "seed" shape should be state transparent.

Any shape that has the property of approximate self-similarity suggests a fractal shape which LOGO can draw.
We insert the recursive calls at each point where we note an approximate reduced image of the whole shape.
Some ferns have this property.
This shape is produced by:

to fern :x if :x<3 [stop] fd :x/12 lt 45 fern 6*:x/16 rt 45 ;There is a "mini-fern" growing at an angle to the main stalk here. fd :x/12 rt 45 fern 6*:x/16 lt 45 fd :x/12 lt 45 fern 5*:x/16 rt 45 fd :x/12 rt 45 fern 5*:x/16 lt 45 fd :x/12 lt 45 fern 4*:x/16 rt 45 fd :x/12 rt 45 fern 4*:x/16 lt 45 fd :x/12 lt 45 fern 3*:x/16 rt 45 fd :x/12 rt 45 fern 3*:x/16 lt 45 fd :x/12 lt 45 fern 2*:x/16 rt 45 fd :x/12 rt 45 fern 2*:x/16 lt 45 fd :x/12 lt 45 fern :x/16 rt 45 fd :x/12 rt 45 fern :x/16 lt 45 fern :x/16 bk :x end

The "seed" for this shape is just a "state transparent" straight line fd :x bk :x which is divided into 12 and then we place a recursive call at 45 degrees alternately right and left. Finally we place a recursive call at the top.

---

Be creative and don't be afraid to experiment. Try inserting recursive calls in various locations in any procedure which is state transparent. You are on your own!

---